Übung 11

Aufgabe 1: Algorithmus von Kruskal

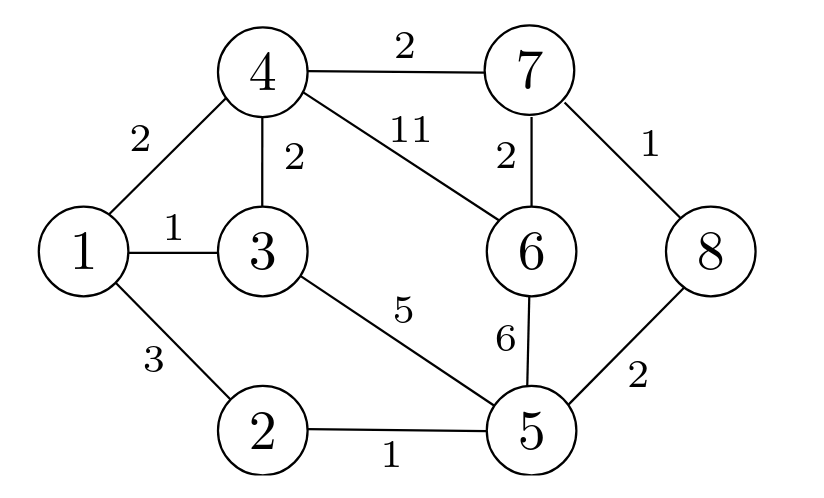
• Nach kruskal sortieren wir nach den Kantengewichten (die Zahlen da an der seite lol)
• Die aufgabe definiert, dass wir das Aufsteigend machen sollen
• Die sind in dieser Reihenfolge:
  • $(1,3),(2,5),(7,8),(1,4),(3,4),(4,7),(5,8),(6,7),(1,2),(3,5),(5,6),(4,6)$
  • erst 1,3, da die näher an 1 dran ist
  • wir sortieren immer nach Gewicht, und dann eben der Lexegographischen Reihenfolge
• Am Anfang haben wir keine Kanten in unserem Baum und für jeden Knoten seine eigene Zusammenhangskomponente
• Das heiß́t, unser baum sieht "mengentechnisch" so aus:
  • $\{1\},\{2\},\{3\},\{4\},\{5\},\{6\},\{7\},\{8\}$
• Wir führen jetzt den Algo von Kruskal aus, so auch in der Klausur notieren:
• Wir fügen also zuerst die Kante zwischen 1 und 3 an und überprüfen, ob diese eine unendliche schleife generiert (einen Kreis verursacht)
  • Tut sie nicht, deswegen fügen wir das dann in unsere Zusammenhangskomponente ein
  • $\text{Zusammenhangskomponente }=\{1,3\},\{2\},\{4\},\{5\},\{6\},\{7\},\{8\}$
  • $T=\{(1,3)\}$
• Einfügen $(2,5)$
  • $\text{Zusammenhangskomponente }=\{1,3\},\{2,5\},\{4\},\{6\},\{7\},\{8\}$
  • $T=\{(1,3),(2,5)\}$
• Einfügen $(7,8)$
  • $\text{Zusammenhangskomponente }=\{1,3\},\{2,5\},\{4\},\{6\},\{7,8\}$
  • $T=\{(1,3),(2,5),(7,8)\}$
• Einfügen $(1,4)$
  • $\text{Zusammenhangskomponente }=\{1,3,4\},\{2,5\},\{6\},\{7,8\}$
  • $T=\{(1,3),(2,5),(7,8),(1,4)\}$
• Einfügen $(3,4)$
  • würde einen Kreis verursachen, nehmen wir daher nicht auf
• Einfügen $(4,7)$
  • $\text{Zusammenhangskomponente }=\{1,3,4,7,8\},\{2,5\},\{6\},$
  • $T=\{(1,3),(2,5),(7,8),(1,4),(4,7)\}$
• Einfügen $(5,8)$
  • $\text{Zusammenhangskomponente }=\{1,3,4,7,8,2,5\},\{6\},$
  • $T=\{(1,3),(2,5),(7,8),(1,4),(4,7),(5,8)\}$
• Einfügen $(6,7)$
  • $\text{Zusammenhangskomponente }=\{1,3,4,7,8,2,5,6\},$
  • $T=\{(1,3),(2,5),(7,8),(1,4),(4,7),(5,8),(6,7)\}$
• Alle folgenden Kanten würden (mind.) einen Kreis verursachen und werden daher nicht aufgenommen
• Das finale $T$ ist dann:
  • $T=\{(1,3),(2,5),(7,8),(1,4),(4,7),(5,8),(6,7)\}$
  • Mit kosten 11, nachdem man das gewicht der Kanten summiert hat

Aufgabe 2: Minimaler Spannwald

a)

• Option A)
  • wir fügen einfach einen neuen knoten an mit den höchsten kosten an jeder kante
  • dann ist das halt das teuerste auf jedem weg, deswegen lohnt sich das dann nich
• Option B)
  • Wir fügen einfach überall wo der Graph nicht zusammenhängt, eine Kante mit relativ hohen Kosten ein $(ma{x}_{kosten}+1)$, damit sich das wie oben wieder nicht lohnt
  • Führe Jarnik-Prim auf diesem "zusammengebauten" Graphen aus
  • Entferne anschliessend die "klebekanten" und spuck das dann aus

Korrektheit:

• Wir zeigen: Der Spannbaum den Janik-Prim auf dem modifizieren Graphen bestimmt, besteht aus
  • einem Spannbaum für jede Zusammenhangskomponente von $G$ und
  • Kanten auf Ê, die zwei Zusammenhangskomponenten verbinden (je höchstens eine pro Paar von Zusammenhangskomponente)

Begründung:

1. Keine Kanten aus Ê werden Innerhalb einer Zusammenhangskomponente verwendet: gilt wegen kreiseigenschaften und Korrektheit Janik-Prim
2. Zwischen zwei Zusammenhangskomponenten wird höchstens eine Kante aus Ê (E-Dach) verwendet

b)

• max Kantengewicht $O(|V|+|E|)$ (Adj, listen)
• Absteigend bei Kante aus $\hat{E}:O(|V|+|E|)\to$ Graph mit $|V|Knoten$
• Janik-Prim $O(|V|log|V|+|E|+|V|-1)\le |E|+|V|-1$ Kanten
• $O(|V|log|V|+|E|)$
• Entfernen den Kanten aus $\hat{E}/E:O(|V|+|E|)$