- Wir wollen uns heute anschauen, wie wir festlegen können, dass etwas entscheidbar ist
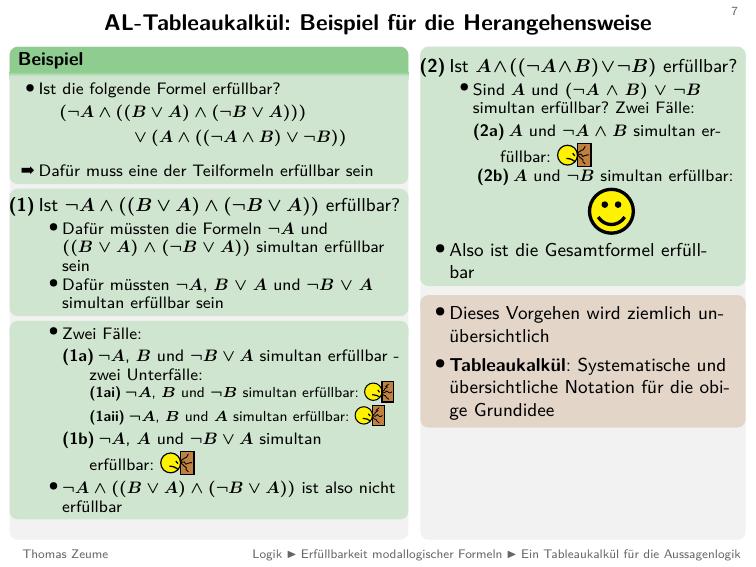
- Wir sehen, dass das nicht besonders übersichtlich ist
- Das ist nicht soooo toll
- Wir schauen uns diesen "tollen" graphen an:
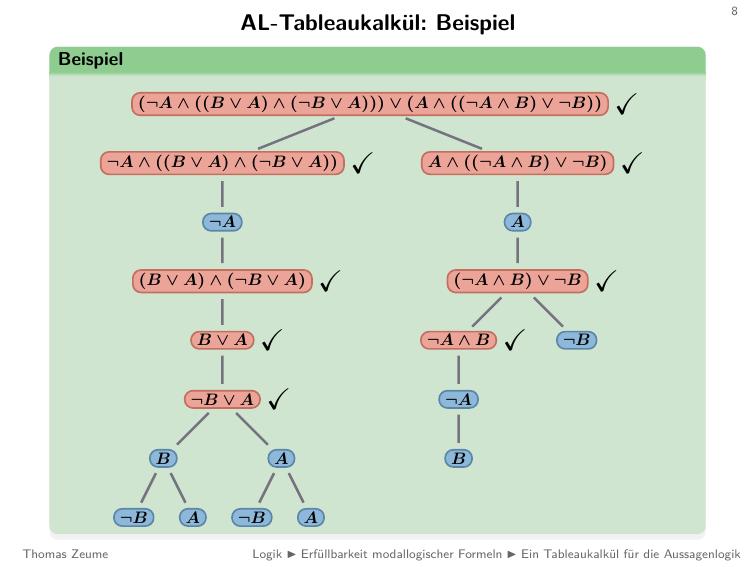
- Damit die Formel erfüllbar ist, muss einer der beiden Formeln wahr sein
- Ein Aussagenlogisches Tableau ist son toller "Baum" dessen knoten so Aussagenlogische Formeln sind
- Ein Tableau für eine AL-Formel ϕ in Negationsnormalform.
- Ohne vorkommen von wahr & falsch kann sie so konstruiert werden:

- Wat bedeutet das denn?
- Ein saturiertes Tableau ist eins, wo alle Knoten die kein Literal sind markiert sind
- [...]

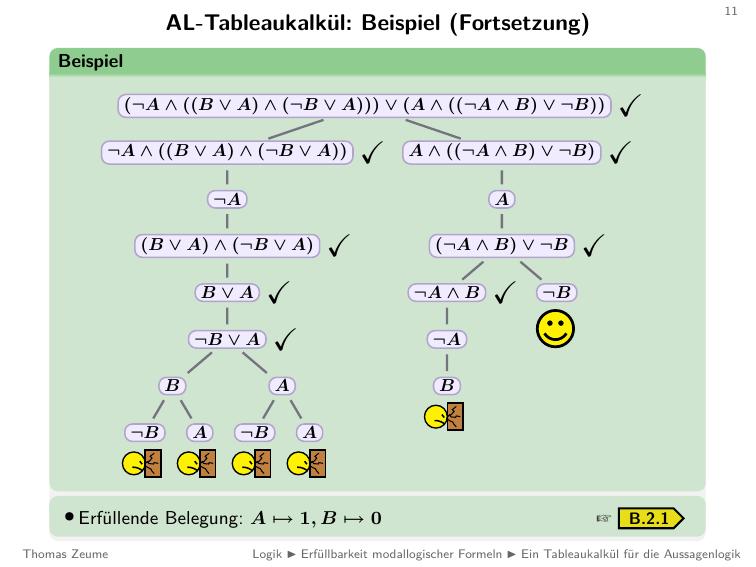
- Wir können das so erreichen, wenn wir die Literale sinnvoll belegen
- (Sinnvoll, ist oben gezeichnet)
- Insgesamt ist das einfach: Wir schauen uns unsere Formel an, und machen "einfach" Fallunterscheidunng
- Das ganze wird hier einfach groß beschrieben
- Wie machen wir das jetzt?
- Wir schauen uns jetzt an, ob unser Algo irgendwann mal terminiert
- Wenn er das nicht machen würde, wäre das deutlich schlecht
- Dann schauen wir, ob das ding jetzt Korrekt ist, und ob das überhaupt das tut, was wir wollen
- Zuletzt schauen wir, ob das was da rauskommt denn überhaupt vollständig ist




