Info Schmei 2: Sortieren

Wir wollen öfter mal kram sortieren
wenn wir kram sortieren müssen wir das mit irgendeiner tollen struktor / einem Algorigthmus machen

Wasn sortieren eigentlich

Wir haben eine beliebig große Menge an Einträgen von beliebiger größe
Wenn wir diese Mege von, sagen wir mal, Zahlen sortieren wollen müssen wir erst etablieren
Was die erwünschte reihenfolge ist
Mit dieser reihenfolge haben wir dann unser ziel zu dem wir sortieren wollen.
Dieser Eintrag (bzw. die Zahl) kann auch Index sein, mit dem man Kram sortieren kann, anstelle davon einfach alleine zu stehen
[We <3 Seni]
Anhand dieser Indizes kann man dann auch sortieren und oder suchen (haha was nen wunder)

Selection Sort
- Wir suchen uns den kleinsten Eintrag der Eingabefolge und verschieben den in die Ausgabefolge
- Und das wiederholen wir bis die Eingabefolge leer ist
- Laufzeit:
Insertion Sort
- schieben den ersten wert der Eingabefolge an die irchtige stelle in der Ausgabe (vor / nach einem bestimmten wert)
- Wiederholen bis die Eingabefolge leer ist
- Laufzeit: Anzahl der Vergleiche $\geq$
- Invariante: die Ausgabefolge enthält vor dem $i$ -ten Durchlauf die $i - 1$ ersten Elemente der Eingabe sortiert.
Mergesort
- Teile und herrsche algorithmus
- Wir teilen unsere eigabe in zwei gleich große teile
- Wir sortieren so lange rekursiv, bis wir nicht mehr sortieren / teilen können
- dann fügen wir am ende die dinger sortiert wieder zusammen
  - Das machen wir am Effizientesten wenn wir
  - in dem wir immer den kleinsten der folge nehmen und anfügen
- Laufzeit:
Quicksort
- Wir suchen uns ein beliebiges Pivot-Element (PIVOOOOOOO)
- Dann vergleichen wir jedes element damit, und sortieren kleinere nach links, größere nach rechts.
- Das machen wir dann rekursiv soooooo oft, bis alles implizit sortiert ist.
- Das cool, weil man kann quicksort gut threaden und damit schneller machen

Algorithmen liefern obere Schranken
Denn wir können relativ einfach, das worst case etablieren
Z.b. Sortieren von $n$ Objektne passiert in $O (n l o g n)$
Die frage ist: Kann man denn überhaupt besser as in $O (n)$ Zeit agieren
- nein, wenn der Algorithmus auf vergleichen aufbaut
- ja, wenn der das nicht tut
Da stellt sich die Frage, wasn dasn eig?
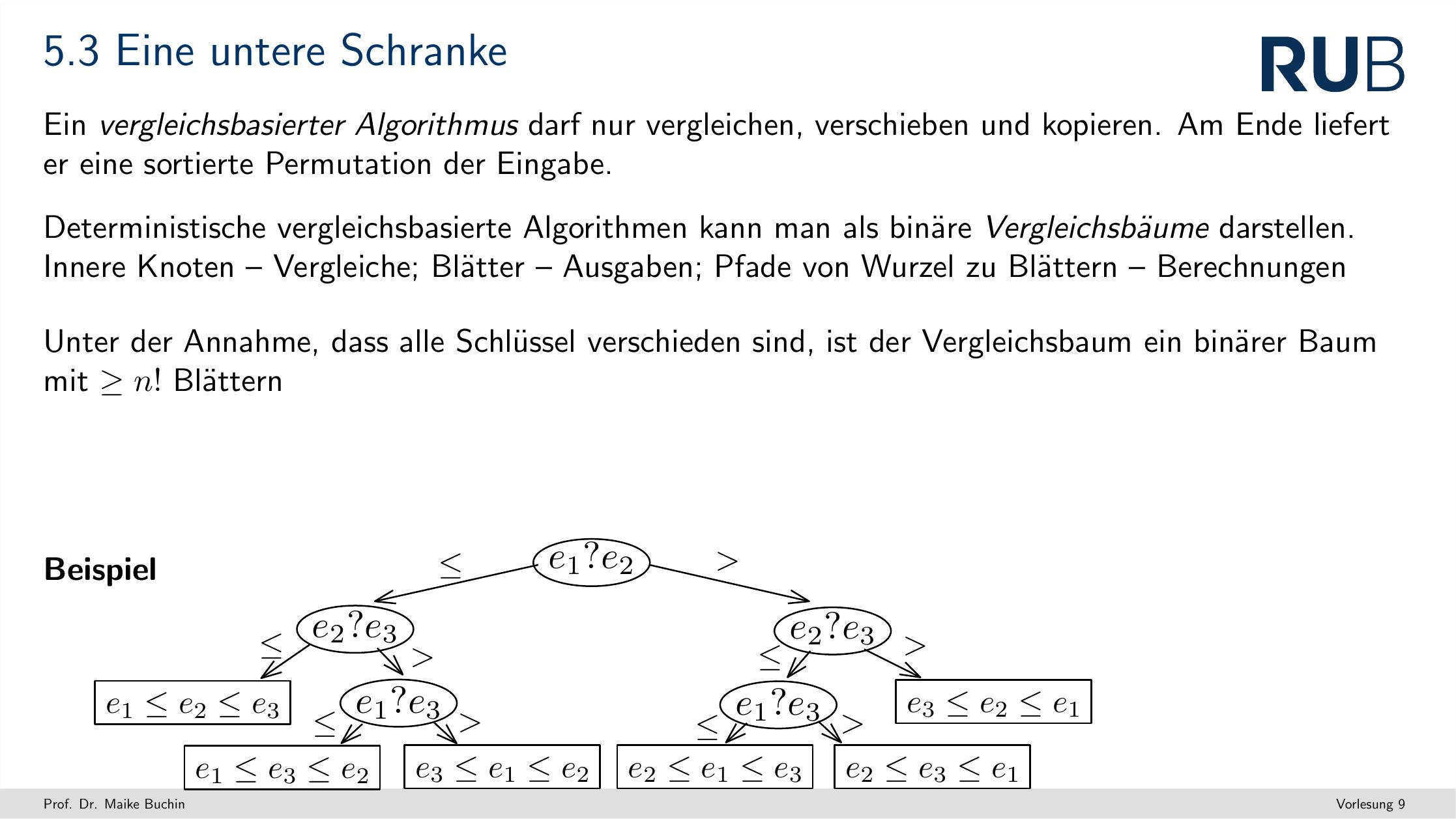
Naja ein vergleichsbasierter Algorithmus darf nur vergleichen, verschieben, und kopieren.
- Das was dabei rauskommt können wir auch "sortierte Permutation" der Eingabe nennen
- Deterministische Vergleichsbarsierte Algorithmen kann man als binary search-trees darstellen
- Wir haben halt den baum, und da entscheiden wir mit rechts oder links, ob das was wir suchen kleiner oder größer als der Derzeitige Knoten ist.
- Wenn wir das alles dann durchmodellerien, haben wir dann einfach "tolle" schlüssel in den blättern
- Wir können so dann aber auch etablieren, dass jeder vergleichsbasierte Sortieralgorithmus im schlechtesten fall $n l o g n - O (n)$ Vergleiche.
- Satz 5.6. Die erwartete Anzahl $C (n)$ von Vergleichen die Quiclsort auf Eingaben mit $n$ einträgen ausführt, erfüllt $C (n) = O (n l o g n)$