Übung 05

Zuerst ein Rückblick

Wir wollen zunächst mal schauen, ob unsere Logiken so vertretbar und oder beweisbar sind

	Erfüllbar	nicht erfüllbar	allgemein gültig	nicht allgemein gültig
nur Aussagenlogik	(Resolution)	Resolution
	DPLL + CDLL	DPLL + CDLL
	Wahrheitstabelle	Wahrheitstabelle	Wahrheitstabelle	Wahrheitstabelle
(nur Hornformeln)	Markierungsalgorithmus	Markierungsalgorithmus
Aussagenlogik & Modallogik	Tableaukalkül	Tableaukalkül	Negierte Formel auf Unerfüllbarkeit testen	Negierte Formel auf Erfüllbarkeit testen
	Modell angeben			nicht erfüllende Interpretation angeben

Resolution
- Es gibt "nur" Exponentiell Viele Klauseln, nicht unendlich
- Dementsprechend kann man mit "brute force" theoretisch alles durchprobieren
- nur weil man das "selber nicht schafft" ist das kein beweis
Beispiel:
- $(A \lor \neg A) \lor (B \land \neg B)$
- Hier sehen wir, dass wir einen geschlossenen Pfad haben, allerdings muss die Formel deswegen nicht allgemeingültig sein
Wir hoffen, dass wir das alles können (yay)

CTL Formeln

Wo gilt welche Formel?

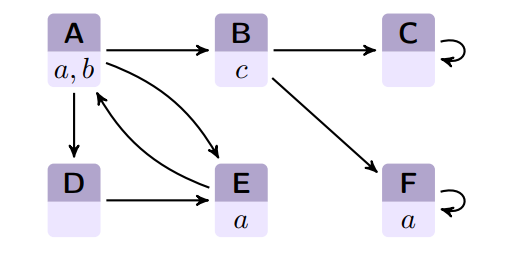
	A	B	C	D	E	F
$E (a U c)$	x	x			x
$EG a$	x				x	x
$A FEG a$	x			x	x	x
$A G a$						x
$EF A G a$	x	x		x	x	x
$FG a$	x			x	x	x
$EG A F a$	x			x	x	x
$EF a$	x	x		x	x	x
$A GEF a$						x

Sind diese Folgen Equivalent?

$A F a \lor A F b$
$A F (a \lor b)$

Modallogik und CTL

a) 1.

CTL
- $a \land ◊ f$
- $a \land EX f$
ML
- Wir können das ggf. einfach nicht auswerten, weil wir theoretisch eine unbeschränkte menge von $□$ -Operatoren brauchen können
- Dadurch ist hier die CTL deutlich ausdrucksstärker, weil $n$ Boxes
- $(f \to \neg a) \land (f \to n \cdot □ \neg a)$

CTL
- $A G (f \to A G \neg a)$
ML
- Wir können das ggf. einfach nicht auswerten, weil wir theoretisch eine unbeschränkte menge von $□$ -Operatoren brauchen können
- Dadurch ist hier die CTL deutlich ausdrucksstärker