Informatik Br(Z)wei: Grundlagen II
- Wir schauen uns in diesem Modul Algorithmen und Datenstrukturen an, damit wir schön sachen modellieren können
- Heute geht es um Laufzeit und Korrektheit
- Wir reden über "tolle" Laufzeiten
- Das ist wie immer super toll
Laufzeiten
- Wenn wir die Laufzeit von etwas ermitteln wollen, dann machen wir das immer in einigen Schritten.
- Wir schauen uns erstmal die Anzahl an elementaren Operationen an
- Wat dat? Variablenzuweisungen, , conditionals
- dann versuchen wir zu ermitteln ob die Laufzeit sich einer änderung der Eingabegröße verändert
- Wir finden solche sachen am besten mit der Asymptotischen Notation heraus
- Wie Sieht das dann aus?:
- time(I) = \text{# Rechenschnritte eines Algorithmus auf einer Eingabe } I
- Analyse im Schlechtesten Fall:
- Alternativ:
- Analyse im besten Fall:
- Analyse im mittleren Fall:
- Analyse im besten Fall:
- All das gilt nur, solange die Menge (dat in den Mengenklammern) endlich ist
- Im allgemeinen betrachten wir die Warscheinlichkeitsverteilung über den Eingaben
- Wir schauen uns erstmal die Anzahl an elementaren Operationen an
- Am ende des tages wollen wir sehr schöne dinge modellieren, mithilfe von diesen sehr schönen Laufzeiten:
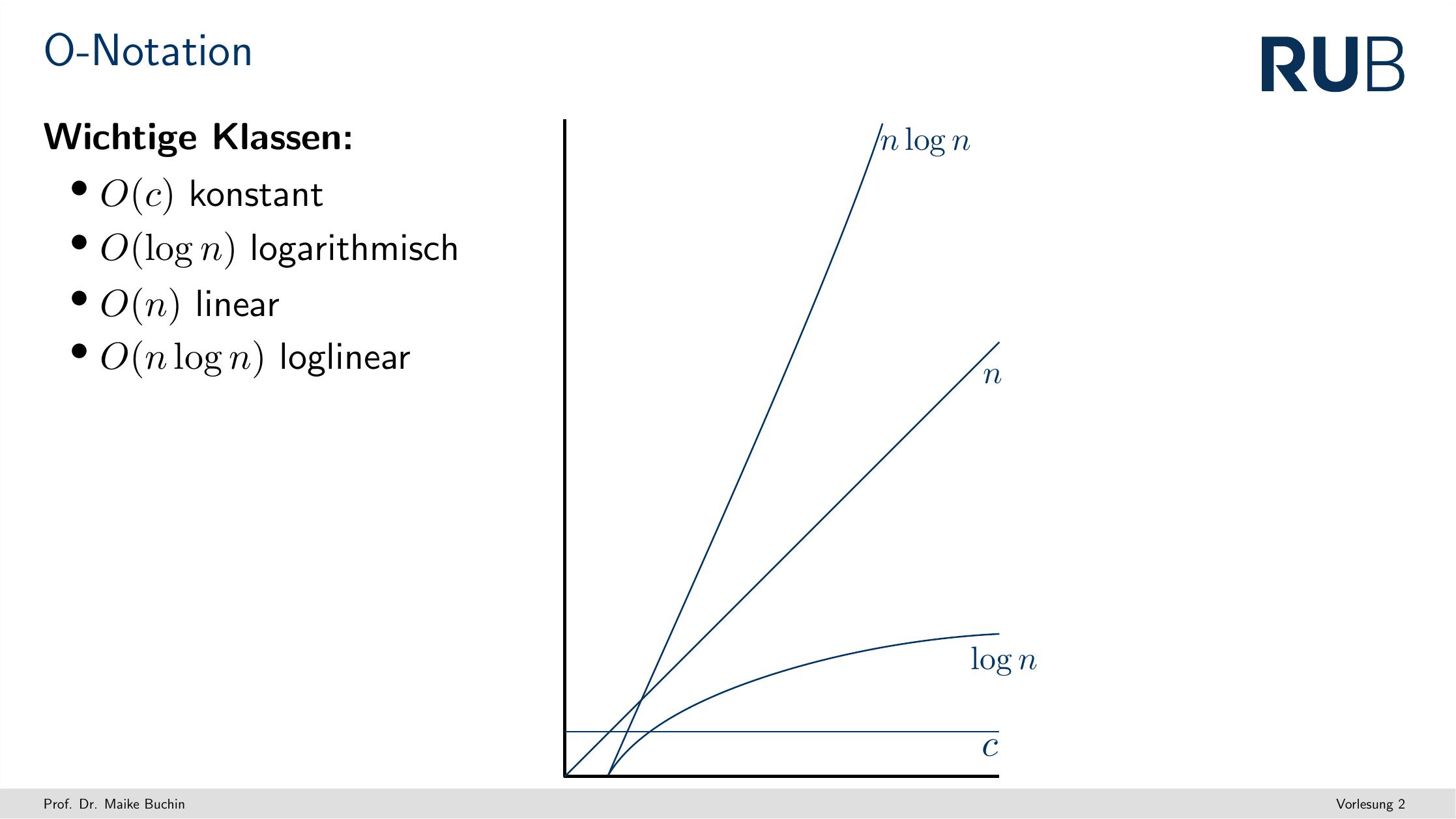
Korrektheit von Algorithmen
- Wenn wir die korrektheit überprüfen wollen, also zeigen wollen, dass etwas das tut was es behauptet zu tun, machen wir das oft mit der sog. Schleifeninvariante
- So heissen Eigenschaften, die vor jedem Durchlauf einer Schleife bzw. einer Wiederholgen Eingabe gelten
- Davon gibt es auch noch nen paar andere Begriffe, deswegen wollen wir hier einmal über alle davon reden:
| Begriff | Erklärung |
|---|---|
| Invariante | Eigenschaften die vor jedem Durchlauf gelten |
| Initialisierung | Eigenschaften die vor dem Ersten durchlauf gelten müssen. Danach können sie weiterhin gelten, müssen dies aber nicht zwingend |
| Aufrechterhaltung | Wenn etwas vor einem Durchlauf gilt, dann gilt das auch danach, Die Aufrechterhaltung kümmert sich darum, dass der Loop weiter loopen kann |
| Terminierung | Die Terminierung beschreibt die Bedingung die erfüllt werden muss, damit die Expression Terminiert werden kann. Diese folgt i.d.R. aus der Invarianten der letzten, vorhergehenden Iteration |
Ein Konkretes Beispiel dafür ist:

