Wir schauen, ob wir unseren kram Zerlegen können (also den automaten)
Wir schauen genauer gesagt, ob wir eine schleife haben, die wir zum "aufpumpen" nutzen können, indem wir sie dauerhauft durchlaufen
Auch wenn wir das n
Das funktioniert übrigens auch, bei begrenzten Sprachen
Wir wollen aber mit dem pumping Lemma herausfinden, wenn irgendetwas nicht regulär ist
Das finden wir heraus, wenn wir einfach den "dann" teil des Pumping-Lemmas invertieren, sprich einfach umdrehen
Dann ist das natürlich aber dann auch nicht regulär
Wir haben eine Sprache mit beliebig vielen as und ms, aber gleich viele
Wir müssen für jedes n
alias mindestens muss der String die Länge n
Wenn wir einen String mit n 2 n
Wichtig ist, dass die Variablen wir wählen, auch immernoch die "regeln" beziehungsweise die "Vorgaben" der Sprache respektiert
In unserem Beispiel reden wir von dem n
Wichtig ist da, dass wir das nicht wählen können, sondern dass uns das von "aussen" angegeben wird
Geanu so gilt das für die Zerlegung
Wir können uns das so vorstellen, dass wir wie zwei Spieler gegeneinander Spielen
Wir versuchen auf der einen Seite alles zusammenzuhalten, und gleichzeitig versucht unser gegenspieler, dass alles wieder kaputt zu machen >:(
Wir können viele dinge einfach über DFAs usw. definieren
Wir schauen uns eine tolle Kaffemaschine an
Die funktioniert nur, wenn wir eine Münze (oder so) eingeworfen haben
Das können wir auch regulär ausdrücken
Erst muss das zeichen für Münze kommen, und dann den rest
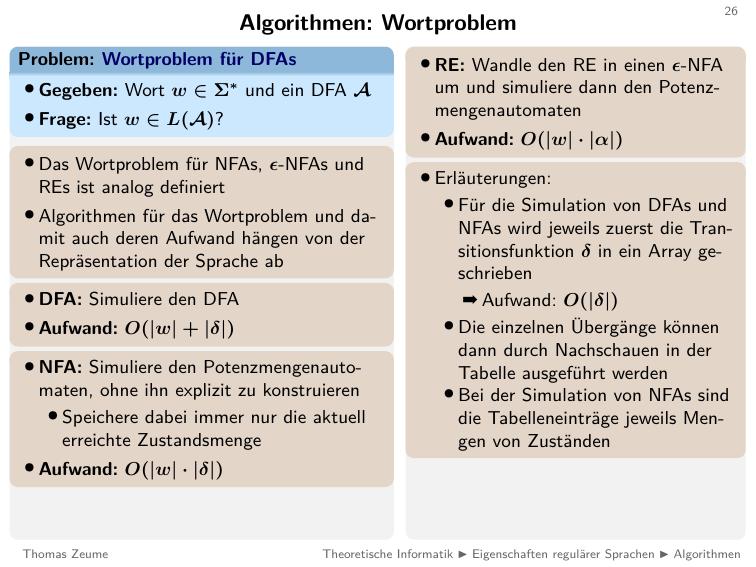
Wie können wir den überprüfen, ob ein Automat die eigenschaften unserer Sprache erfüllt?
Wir müssen sicher gehen, dass alle wörter die der Automat akzeptiert, auch in unserer Sprache liegen
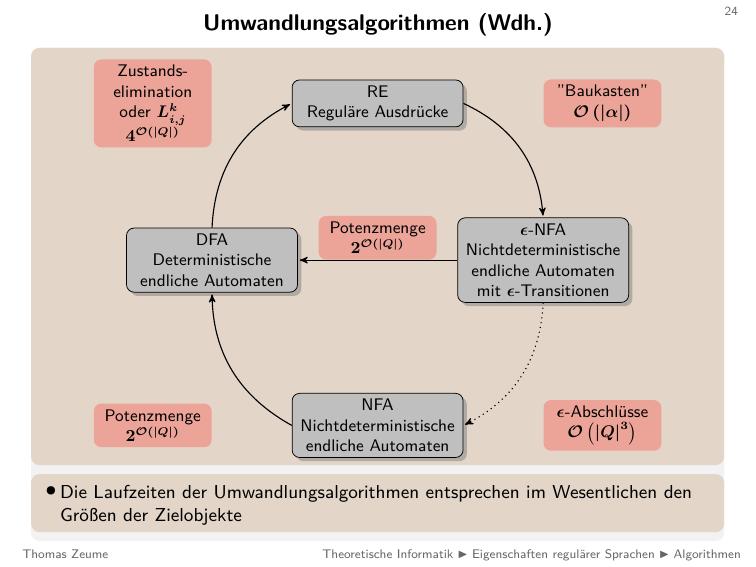
Wenn wir uns das so anschauen, wäre es schon sehr cool eine "Toolbox" zu haben, aus der wir "Bausteine" kopieren könnten
Achja und testen bestimmt jaja
Wie machen wir jetzt aus einem Regex einen Automaten?
Wir wollen das, damit wir das "einfacher" berechnen können
Interessant ist für uns folgendes:
Wir denken uns erstmal unseren Boolsche dinge
Damit wir das vernünftig verarbeiten können, muss man
den durchschnitt zwischen zwei als regulär einstufen können
und ein Komplementär ebenfalls
Ausserdem sollten die operationen mögloichst effizient ausgeführt werden
Wir können diese tollen automaten ja auch umziehen
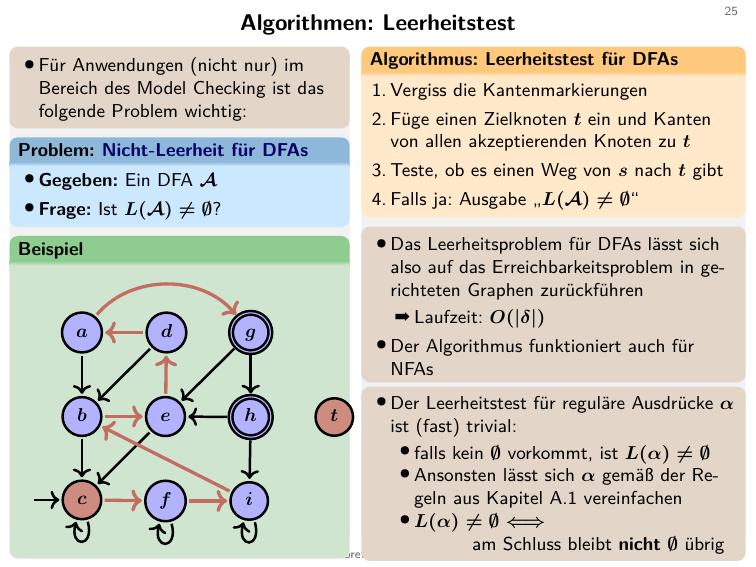
Wir wollen erstmal schauen, ob nen Automat leer ist, denn wenn ein Automat leer ist (keine transaktionen hat) können wir logischerweise auch nichts sinnvolles damit machen
Wir betrachten zwei automaten
Wir wollen wissen, ob die beiden Equivalent sind
Wir bauen erstmal einen tollen Produktautomaten, für jeden DFA den wir inspizieren wollen
Dann entfernen wir alle Zustände die nicht erreichbar sind
Wenn die beiden Sprachen äquivalent sind, dann sind die beiden Automaten auch äquivalent